
Research Topic: Correlation of space debris observations and collision avoidance
Many available techniques to solve orbit determination problem are very precise and reliable. Regarding the consequences of the space debris environment, an efficient collision avoidance in terms of time has to be performed.
Therefore, we need to compute propagation of orbits to predict possible future conjunctions between Earth satellites but it requires good algorithms in terms of computational complexity. Thus, polynomial formulations of the preliminary orbit determination problem are studied.
With this project, we investigate new algorithms to determine the initial orbit of space debris starting from optical/radar observations. Moreover, the research conducts to the development of new techniques to detect pairs of satellites with possible collision in the near future. Indeed, we study a method which uses the evolution of the trajectories to filter pairs of objects that need further investigation in the collision avoidance procedure.
Main Results:
In G. F. Gronchi et al 2015 (see References), we introduce a new algorithm to define the preliminary orbit of LEO satellites based on radar observations with defined specifications of the instrument and observation scheduling.
It consists in performing the "linkage" operation, i.e. joining the data of two radar tracks of four observations with a dynamical model, allowing to compute one or more preliminary orbits. This method takes advantage that the deviations of the right ascension and declination are small, and solves the equations from the five algebraic integrals of Kepler’s problem, the Lambert’s theorem for elliptic motion and from the motion of the satellite projected into the line of sight. In the paper, we describe two approaches of this so-called “Infinitesimal Angles method”: one uses linear equations (IAL), the other one works with quadratic equations (IAQ).
Assuming no perturbations on the motion of observed satellites, we perform numerical tests to evaluate the new method and compare with Keplerian integrals (KI) and Gibbs’ method (G).
Two tracks of simulated observations are generated with a two-body propagation for a virtual object (see Table 1) where we added errors according to the five test cases described in Table 2.
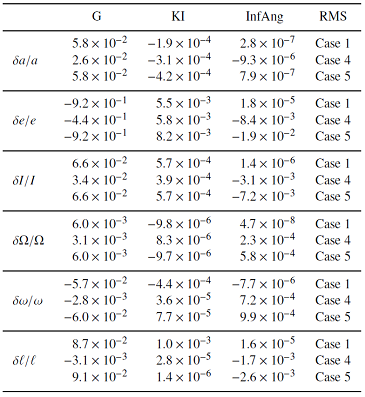
Note that in Case 1 for IAL and IAQ (see respectively Tables 3 and 4), this new technique is able to correct the errors in the angles and to recover the orbital elements of the test orbit, considering exact value of the range.
If we add errors in the observations of the range, the value of the semi-major axis computed by IAQ is better but it is slightly worse for the other elements comparing with KI (see Cases 4 and 5 of Table 4).
The next step of the research is to include the effect of Earth oblateness in this given preliminary orbit determination problem to test the efficiency of the new technique, considering the first order secular terms of J2 coefficient. Moreover, we hope in the near future to perform numerical tests in large scale and if possible, with real observations.
Table 1:
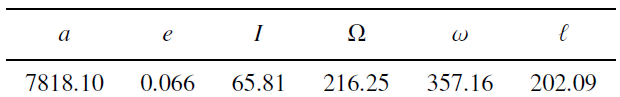
Table 2:
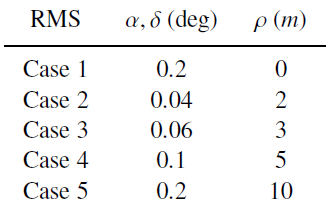
Table 3: Table 4:

References:
Article: G. F. Gronchi, L. Dimare, D. Bracali Cioci, and H. Ma On the computation of preliminary orbits for Earth satellites with radar observations, MNRAS (August 01, 2015) Vol. 451 1883-1891. (link: http://mnras.oxfordjournals.org/content/451/2/1883.abstract)
Talk: G. F. Gronchi, L. Dimare, D. Bracali Cioci, and H. Ma, Comparison of different methods to compute a preliminary orbit of space debris with radar observations, 310 IAU-Symposium, Complex Planetary Systems, Namur, July 2014.
Proceedings: H. Ma, G. F. Gronchi, 2014, in Complex Planetary Systems, Vol. 9 of Proceedings of the International Astronomical Union, Comparison of different methods to compute a preliminary orbit of space debris using radar observations, pp 154–155.
Resources:
Linkedin Profile webpage: https://it.linkedin.com/in/mahelene