1- Research topic

Uncertainty propagation in orbital mechanics is a key enabling technology that is at the basis of all orbit determination, state estimation, guidance, navigation and control, impact and collision prediction processes. In particular, in the case of space debris orbit analysis, uncertainty propagation is required to predict possible collisions or to describe the evolution of a cloud of particles. The evolution of an uncertainty region can be described through a linear model by multiplying the variation of the uncertain variables by the state transition matrix of the linearized dynamics. However, it can be shown that this approach is not suitable to correctly represent the evolution of an uncertainty region even over a short period of time. For this reason, in recent times, authors have proposed higher order methods either intrusive or non-intrusive. Intrusive approaches for uncertainty quantification are methods that require a modification of either the system model or the algebra used to evaluate the quantities of interest. The most popular uses Taylor series expansions and differential algebra. Instead, the main advantage of non-intrusive methods is in the ability to work with generic models, also in the form of black-boxes, and with little requirements on the coding of the models or on their regularity.

2- Main research

In [1] we compare four different non-intrusive approaches applied to the propagation of uncertainty in orbital dynamics under different orbit regime and uncertainty both on the orbital parameters and dynamical models. The approaches are: a Polynomial Chaos Expansion (PCE), an Uncertainty Quantification-High Dimensional Model Representation (UQ-HDMR) a Generalized 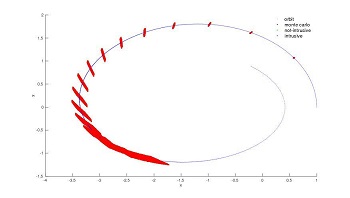Kriging model and an polynomial expansion with Tchebycheff polynomials on sparse grids. The uncertainty on the dynamical parameters increase the non-linearity of the uncertainty region, and higher order polynomials are needed. UQ-HDMR provided comparatively good results on all test functions at a computational cost comparable to the Tchebycheff approximation on sparse grids.

In [2] we present the algebra of Tchebycheff polynomials on Tchebycheff basis applied to the propagation of uncertainties in astrodynamics. It is a first step towards the definition of a Generalised Intrusive Polynomial Expansion (GIPE) technique for uncertainty propagation. The intrusive method has been also compared to its non intrusive counterpart: the Tchebycheff polynomial interpolation on sparse grid.

In [3] we present a nonlinear approach to the design of optimal collision avoidance and re-entry maneuvers considering both aleatory and epistemic uncertainty in initial conditions and model parameters. To reduce the computational cost of the optimization, we substitute the true 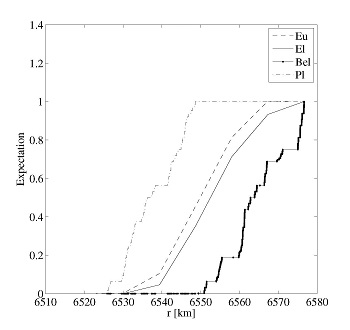 dynamics with its approximation based on multivariate Tchebycheff polynomial expansion. The polynomial expansion represents a nonlinear mapping between the initial uncertainty space and the terminal conditions. The assumption of perfectly known a priori probability distributions has been dropped, instead, sets of probability measures has been considered. The expectation of a collision is then computed considering all the pieces of evidence supporting the proposition that an intersection between the area defining all possible terminal positions of a spacecraft and a control volume is an empty set. An inverse proposition holds for the expectation of a re-entry event.


3- References

[1] C. Tardioli, M. Kubicek, M. Vasile, E. Minisci and A. Ricciardi, Comparison of non-intrusive approaches to uncertainty propagation in orbital mechanics, AAS Astrodynamics Specialists Conference, Vail, Colorado, USA, August 9--13, 2015. AAS 15-545

[2] A. Riccardi, C. Tardioli and M. Vasile, An intrusive approach to uncertainty propagation in orbital mechanics based on Tchebycheff polynomial algebra, AAS Astrodynamics Specialists Conference, Vail, Colorado, USA, August 9-13, 2015. AAS 15-544

[3] C. Tardioli and M. Vasile, Collision and re-entry analysis under aleatory and epistemic uncertainty, AAS Astrodynamics Specialists Conference, Vail, Colorado, USA, August 9-13, 2015. AAS 15-709