Research topic:
My main research interest is in improving orbit propagation techniques of asteroids and space debris by employing regularized formulations of orbital dynamics.

I am applying regularized element methods [1,2,3,4,5,6] to the numerical propagation of interplanetary trajectories that involve a close encounter with a major body, such as those of near-Earth-asteroids (NEAs) and spacecraft undertaking gravity assist manoeuvres. Close encounters are a possible pathway to chaotic dynamics, since small initial distances between trajectories are amplified. Sequences of encounters lead to the exponential divergence of such trajectories [7], which is one of the defining characteristics of chaotic systems. In this context, efficient and reliable numerical propagation techniques are of key importance in a number of situations, ranging from statistical studies of chaotic systems to interplanetary mission design and trajectory optimization.
I am comparing the performances of novel semi-analytical and numerical methods in the propagation of space debris with the aim of finding a balance between computational cost and accuracy for a variety of applications such as the evolution of large debris populations, lifetime predictions and conjunction analyses.
As an additional line of research, I am also working on asteroid impact risk assessment during and after an asteroid deflection action performed with slow-push methods.
REFERENCES:1. Stiefel E. L., Scheifele G., “Linear and Regular Celestial Mechanics”. Springer-Verlag Heidelberg Berlin, 1971.
2. Peláez J., Hedo J. M., Rodríguez de Andrés P., “A special perturbation method in orbital dynamics”. Celest. Mech. Dyn. Astr., Vol. 97(2), 2007.
3. Baù G., Bombardelli C., Peláez J., “A new set of integrals of motion to propagate the perturbed two-body problem”. Celest. Mech. Dyn. Astr., Vol. 116(1), 2013.
4. Baù G., Bombardelli C., “Time elements for the enhanced performance of the Dromo orbit propagator”. Astron. J., 148, 2014.
5. Roa J., Peláez J., “Orbit Propagation in Minkowskian geometry”. Celest. Mech. Dyn. Astr., 123(1), 2015.
6. Baù G., Bombardelli C., Peláez J. et al., “Non-singular orbital elements for special perturbations in the two-body problem”. Accepted for publication in Mon. Not. R. Astron. Soc., 2015.
7. Valsecchi G. B., Milani A., Gronchi G. F. et al., "Resonant returns to close approaches: Analytical theory". Astron. Astrophys., 408, 2003.
Main results1. Mitigation of propagation error in interplanetary trajectories
Interplanetary trajectories that involve two subsequent Earth close encounters were propagated by decomposing them into heliocentric and geocentric phases. In each of these the trajectory was propagated using a regularized formulation of the equations of motion, taking into account a restricted circular three-body problem. The trajectories were designed as to accurately simulate those followed by NEAs undergoing resonant Earth close encounters. The initial conditions were chosen as to obtain two successive close encounters, the second following the first by 7 years and 8 particle periods (7:8 resonance), and the positional error was measured in the (\xi, \zeta) b-plane coordinates of the second encounter. As to measure the computational cost of each integration, the number of function calls to the right-hand side of the equations of motion was registered for each integration. The number of function calls vs. positional error in the b-plane coordinates of the second encounter is plotted in Figure 1 for three initial eccentricities of the heliocentric orbit.
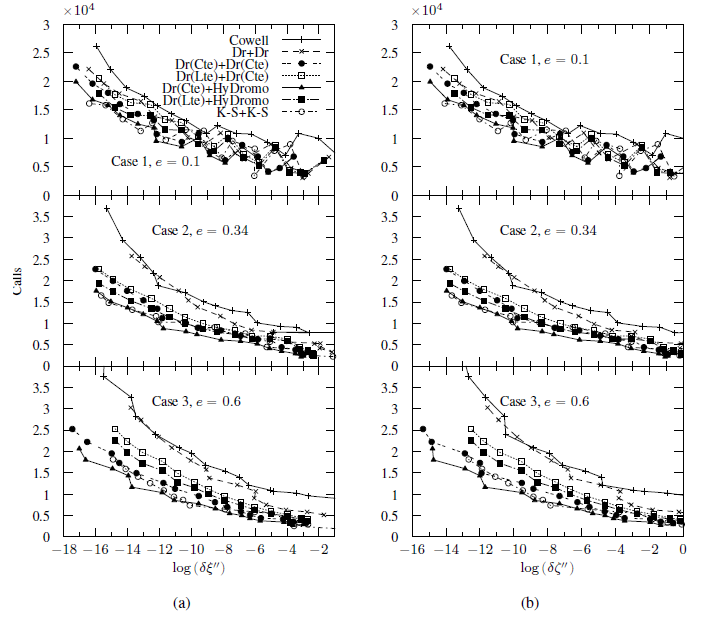
[FIG. 1: Number of function calls vs. relative positional error in the b-plane coordinates for three different initial eccentricities of the heliocentric orbit. Figure a) is relative to errors in \xi, figure b) to errors in \zeta. Each curve refers to a different combination of formulations used in the heliocentric and geocentric phases, i.e. “a+b” refers to formulation “a” in the heliocentric phase and formulation “b” in the geocentric phase. For description of the abbreviations refer to reference].
The advantage of using regularized formulations instead of Cowell’s method (the integration of Newtonian equations of motion in time) is readily apparent, since they allow to cut the computational cost for the same accuracy by a factor of up to three. The trends are similar for both the \xi and \zeta b-plane coordinates, with errors in \zeta being two orders of magnitude greater than those in \xi due to the divergence of the trajectories after the first close encounter.
REFERENCE: Amato D., Bombardelli C., Baù G., “Mitigation of propagation error in interplanetary trajectories”. Paper no. AAS15-355 in Proceedings of the 24th AAS/AIAA Spaceflight Mechanics Meeting, Williamsburg, VA, USA, 2015.
2. Ion beam deflection of fictitious asteroid 2015PDC
A short-warning asteroid deflection mission using the ion beam shepherd slow-push deflection method was designed for the 250m fictitious impactor 2015PDC, whose impact scenario (http://neo.jpl.nasa.gov/pdc15/) was presented at the 2015 Planetary Defense Conference. The mission was designed as to achieve a partial deflection of the asteroid and shift its nominal ground impact point away from populated areas, thereby dramatically reducing the costs of evacuation and infrastructural damage. These are evaluated by integrating the population density and the light intensity from a high-resolution night image of the Earth in a 100km-radius circle centred on the nominal impact point, which shifts along the risk corridor during the whole deflection period (Figure 2).
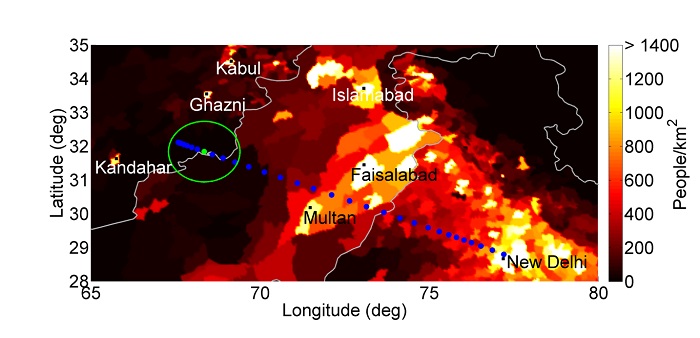
[FIG. 2: Shifting of the impact point from a nominal impact close to New Delhi, India towards sparsely populated regions at the Afghanistan-Pakistan border. Lighter colours correspond to higher population densities.]
REFERENCE: Bombardelli C., Amato D., Cano J. L., “Mission Analysis for the Ion Beam Deflection of Fictitious Asteroid 2015 PDC”. Accepted for publication in Acta Astron., 2015.